PHP实现二叉树
树
我们知道常见的数据结构,如:链表、栈、队列,从物理上或者逻辑上来说,存在一定的前后次序,并且前驱和后继是唯一的,因此称之为线性结构。然而,实际上,链表的循秩访问等的操作,复杂度都相对高。而树的数据结构,可以把两种结构的优势结合起来。
与线性结构不同,树不存在天然的直接后继或者直接前驱关系,不过,我们可以通过自己定义一些约束,在树中确定节点之间的线性次序。
树属于半线性结构。树也由一组顶点以及之间的联边组成,外加指定一个特定的根节点。
二叉树
如果每个节点最多有两个孩子,即每个节点的度数均不超过2,称为二叉树。
二叉树中,如果同一节点的孩子以左右区分,称为有序二叉树。特别地,不含一度节点的二叉树称作真二叉树。二叉树是不失一般性地,比如一个多叉树,如果可以定义兄弟节点的次序,那么可以转换为一颗二叉树。
图
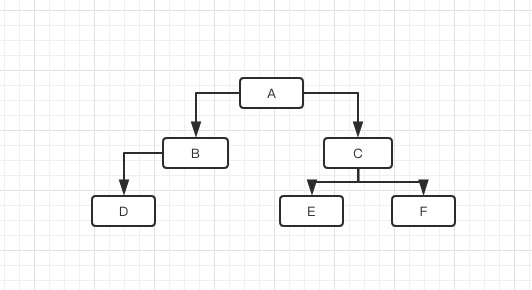
tree-two-20180915.jpg
代码
class Node{
public $value;
public $left;
public $right;
}
//先序遍历
function Firstorder($root){
$stack = [];
array_push($stack,$root);
while(!empty($stack)){
$center_node = array_pop($stack);
echo $center_node->value.' ';
if($center_node->right != null){
array_push($stack,$center_node->right);
}
if($center_node->left != null){
array_push($stack,$center_node->left);
}
}
}
//中序遍历
function Middleorder($root){
$stack = [];
$center_node = $root;
while (!empty($stack) || $center_node != null) {
while ($center_node != null) {
array_push($stack, $center_node);
$center_node = $center_node->left;
}
$center_node = array_pop($stack);
echo $center_node->value . " ";
$center_node = $center_node->right;
}
}
//后序遍历
function Afterlorder($root){
$stack = [];
$outstack = [];
array_push($stack,$root);
while(!empty($stack)){
$center_node = array_pop($stack);
array_push($outstack,$center_node);
if($center_node->left != null){
array_push($stack,$center_node->left);
}
if($center_node->right != null){
array_push($stack,$center_node->right);
}
}
while(!empty($outstack)){
$center_node = array_pop($outstack);
echo $center_node->value.' ';
}
}
$a = new Node();
$b = new Node();
$c = new Node();
$d = new Node();
$e = new Node();
$f = new Node();
$a->value = 'A';
$b->value = 'B';
$c->value = 'C';
$d->value = 'D';
$e->value = 'E';
$f->value = 'F';
$a->left = $b;
$a->right = $c;
$b->left = $d;
$c->left = $e;
$c->right = $f;
Firstorder($a);
echo '<br/><br/><br/>';
Middleorder($a);
echo '<br/><br/><br/>';
Afterlorder($a);
//输入分别是
//A B D C E F
//D B A E C F
//D B E F C A