算法之时间复杂度
通常对于一个程序复杂逻辑需要用到算法来解决的地步,选用什么样的算法便成为了程序员需要头疼的事情,那么对于算法选择我们该如何分析。通常来讲我们需要做两项分析。
第一步是从数学上证明算法的正确性,这一步主要用到算式证明的方法及相关推理模式,如循环不变式、数学归纳法等。
而在证明算法是正确的基础上的第二步就是分析算法的时间复杂度。算法的时间复杂度反映了程序执行时间随输入变量的规模增长而增长的量级,在一定程度上能反映出算法的优劣。因此,作为程序员,掌握基本的算法时间复杂度分析方法是很有必要的。
时间复杂度首先要知道一个点,就是语句频度,也叫时间频度。顾名思义,就是一个算法中语句的执行次数。我们通常记为T(n)
在前面说的时间频度中我们能够知道就是,当n这个值也就是问题规模发生变化的时候,时间频度T(n)也随之发生变化,但是我们若是想知道究竟是发生什么变化的时候,时间复杂度的概念也就随之而来。
在一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
而T(n)=O(f(n))中存在一个常数C,使得在当n趋于正无穷时T(n)≤C*f(n)。简单来说,就是T(n)在n趋于正无穷时最大也就跟f(n)差不多大。也就是说当n趋于正无穷时T(n)的上界是C*f(n)。其虽然对f(n)没有规定,但是一般都是砍掉常数,系数。
所以,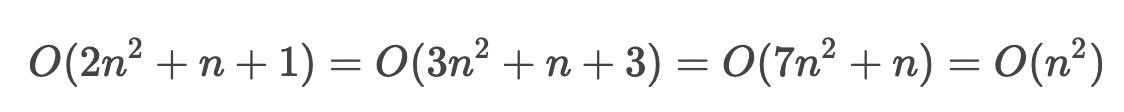
2020-09-18-01.jpg
for($i = 1;$i <= $n;$i++){
$x++;
}
for($i = 1;$i <= $n;$i++){
for ($j = 1;$j <= $n;$j++){
$x++;
}
}
第一个for循环的时间复杂度为Ο(n),第二个for循环的时间复杂度为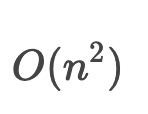
2020-09-18-02.jpg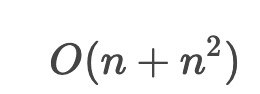
2020-09-18-03.jpg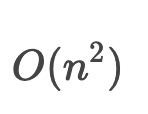
2020-09-18-02.jpg